Electrostatic Potential (Quantum Espresso) - Courtesy of Andrew Doyle
#######################################################
## Tutorial by: Andrew
## Topic: Electrostatic potential in ase-espresso
##
## dependencies: ase, espresso, pickle
##
## Generates the data files necessary to analyze
## the charge density and electrostatic potential
## in and around a Pt(100) slab
#######################################################
# Import necessary packages
from ase import Atoms
from ase.io import write
from ase.lattice.surface import fcc100
from espresso import espresso
import pickle
# Generate the representation of the atoms in ASE
slab = fcc100('Pt', size=(2,2,3), vacuum=10.0)
# Create an espresso calculator object
# (Tailor for desired settings and accuracy)
calc = espresso(pw=400 , # Plane wave cutoff
dw=4000, # Density wave cutoff
kpts=(3,3,1), # (rather sparse) k-point (Brillouin) sampling
xc='RPBE', #Exchange-correlation functional
dipole={'status':True}, # Includes dipole correction (necessary for asymmetric slabs)
outdir='pt100_analysis') # Espresso-generated files will be put here
# Attach the calculator object to the atoms
slab.set_calculator(calc)
# Perform a static calculation to generate wavefunctions
slab.get_potential_energy()
# Create an image of the atoms
write('slab.png',slab)
# Get the electrostatic potential
potential = calc.extract_ionic_and_hartree_potential()
# Create and populate output file for electrostatic potential
potential_file=open('potential.pickle','w')
pickle.dump(potential,potential_file)
potential_file.close()
Now we are done with the intensive calculations. The following scripts will interpret the results and can be run easily on any computer in a matter of seconds.
#######################################################
## Tutorial by: Andrew
## Topic: Plotting electrostatic potential data from
## ase-espresso
##
## dependencies: pickle, pylab, numpy
##
## Plots an XY-averaged electrostatic potential as
## a function of Z position through and outside
## a Pt(100) slab.
#######################################################
# Import necessary packages
import pickle
import pylab as plt
import numpy as np
# Retrieves the data generated in the previous script
potential_file = open('potential.pickle')
potential = pickle.load(potential_file)
origin=potential[0] # [X0,Y0,Z0] - The positions of the origin of the cell. Here they are [0,0,0]
cell = potential[1] # [3x3 Matrix] Contains the [x,y,z] components of the 3 cell vectors
cell_x = cell[0][0] # The x component of the first cell vector (Remember: This cell is rectangular)
cell_y = cell[1][1] # The y component of the second cell vector (Remember: This cell is rectangular)
cell_z = cell[2][2] # The z component of the third cell vector (Remember: This cell is rectangular)
v = potential[2] # Contains all real-space potential field points.
#######################################################
## Understanding the architecture of the rest of the
## data can be tricky. Using the variables presented
## here, V(x,y,z)=v[x][y][z].
##
## First we aim to extract all the information
## available to us, based on numpy's architecture.
#######################################################
n_x = len(v) # Returns the number of entries in the first subset (number of X entries)
n_y = len(v[0]) # Returns the number of entries in the second subset (number of Y entries - choice of '0' was arbitrary)
n_z = len(v[0][0]) # Returns the number of entries in the third subset (number of Z entries - choice of '0' was arbitrary)
potential = [] # Initializes a list for average potentials
# Iterate over all space to average and process potential information
for z in range(n_z):
temp = 0 # Will serve as a partial sum for averaging purposes
for x in range(n_x):
for y in range(n_y):
temp+=v[x][y][z] # Sums the potential at all points in an X-Y plane
temp = temp / (n_x*n_y) # Divides by the total number of points
potential.append( temp ) # Stores the value for average potential at this Z position
# Translates the indices of points along the Z axis into real-space positions
z_coordinate = np.linspace( 0 , cell_z , n_z )
# Plots the data, formats plot
plt.plot(z_coordinate, potential)
plt.xlabel(r'z ($\AA$)',size=18)
plt.ylabel(r'$\langle V \ \rangle_{XY}$ (Volts)',size=18)
plt.title('Electrostatics of Pt(100)',size=18)
# Display plot
plt.show()
# If you'd prefer to save the plot, highlight the line above and uncomment the line below
#plt.savefig('potential_analysis.png')
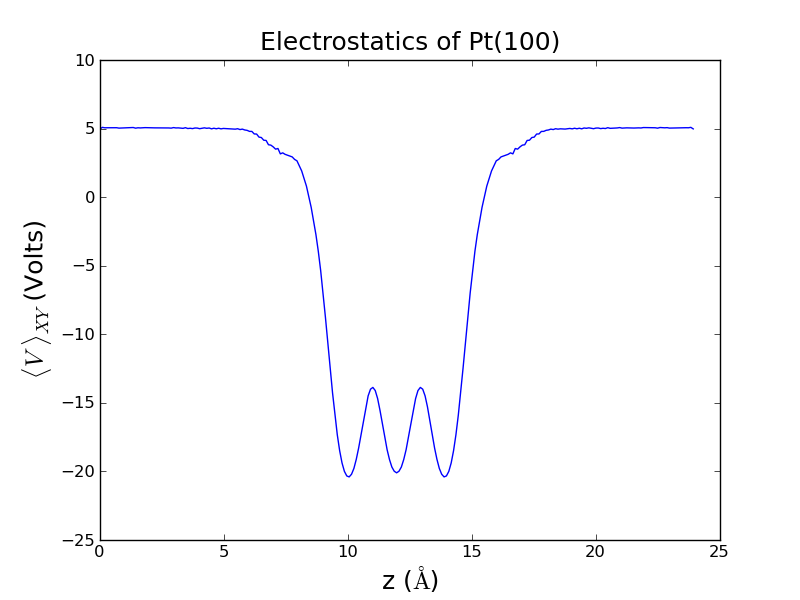
The end result should look something like this:

Plot self-consistent field convergence data
This script, when run in a quantum espresso job folder, will plot the estimated SCF accuracy and total DFT energy as a function of electronic step. This can be useful for diagnosing weird convergence behavior, or for impatiently waiting for the next ionic step to finish.
#!/home/vossj/suncat/bin/python
import os
import pylab as plt
import sys
import matplotlib.pyplot as plt2
from mpl_toolkits.axes_grid1 import host_subplot
import mpl_toolkits.axisartist as AA
rydberg = 13.6057 #rydberg to eV conversion
# default to outdir/log if no log is given
if len(sys.argv) > 1:
log = sys.argv[1]
else:
log = 'outdir/log'
filename = 'scf_temp.txt'
filename2 = 'etmp.txt'
os.system('grep scf %s > %s'%(log,filename))
os.system("grep 'total energy' %s > %s"%(log,filename2))
file = open(filename)
lines = file.read().split('\n')
lines = filter(None,lines)
file2 = open(filename2)
lines2 = file2.read().split('\n')
lines2 = filter(None,lines2)
scf = []
energy = []
iter = []
iter2 = []
n = 0
# append scf convergence data from log file to scf
for line in lines:
items = filter(None, line.split(' '))
try:
scf.append( float(items[4])*rydberg )
n += 1
iter.append(n)
except:
continue
# append total dft energy data from log to energy
n = 0
for line in lines2:
items = filter(None, line.split(' '))
try:
n += 1
energy.append(float(items[3])*rydberg )
iter2.append(n)
except:
continue
# find the plane-wave cutoff from the log file
os.system("grep 'kinetic-energy cutoff' %s > %s"%(log,filename))
file = open(filename)
items = filter(None, file.read().split(' '))
pw = float(items[3]) * 13.606
os.system('rm %s'%filename)
os.system('rm %s'%filename2)
# plot everything nicely
host = host_subplot(111,axes_class = AA.Axes)
plt2.subplots_adjust(right=0.75)
par1 = host.twinx()
host.set_xlabel('Number of Iterations')
host.set_ylabel('Estimated SCF Accuracy (eV)',color='red')
par1.set_ylabel('DFT Total-Energy (eV)',color='green')
p1, = host.plot(iter,scf,label='SCF Acc')
p2, = par1.plot(iter2,energy,label='DFT Energy')
host.set_yscale('log')
plt.semilogy(iter,scf)
plt.xlabel('Number of Iterations')
plt.ylabel('Estimated SCF Accuracy (eV)')
plt.title(r'$PW_{Cut}$=%d eV'%pw)
plt.tight_layout()
plt.show()
The output should look something like this, for a nicely converging run with several ionic steps. Multiple ionic step directories will contain all ionic steps in the plot.