The following script generates and saves the electrostatic potential data.
####################################################### ## Tutorial by: Andrew ## Topic: Electrostatic potential in ase-espresso ## ## dependencies: ase, espresso, pickle ## ## Generates the data files necessary to analyze ## the charge density and electrostatic potential ## in and around a Pt(100) slab ####################################################### # Import necessary packages from ase import Atoms from ase.io import write from ase.lattice.surface import fcc100 from espresso import espresso import pickle # Generate the representation of the atoms in ASE slab = fcc100('Pt', size=(2,2,3), vacuum=10.0) # Create an espresso calculator object # (Tailor for desired settings and accuracy) calc = espresso(pw=400 , # Plane wave cutoff dw=4000, # Density wave cutoff kpts=(3,3,1), # (rather sparse) k-point (Brillouin) sampling xc='RPBE', #Exchange-correlation functional dipole={'status':True}, # Includes dipole correction (necessary for asymmetric slabs) outdir='pt100_analysis') # Espresso-generated files will be put here # Attach the calculator object to the atoms slab.set_calculator(calc) # Perform a static calculation to generate wavefunctions slab.get_potential_energy() # Create an image of the atoms write('slab.png',slab) # Get the electrostatic potential potential = calc.extract_total_potential() # Create and populate output file for electrostatic potential potential_file=open('potential.pickle','w') pickle.dump(potential,potential_file) potential_file.close()
Now we are done with the intensive calculations. The following scripts will interpret the results and can be run easily on any computer in a matter of seconds.
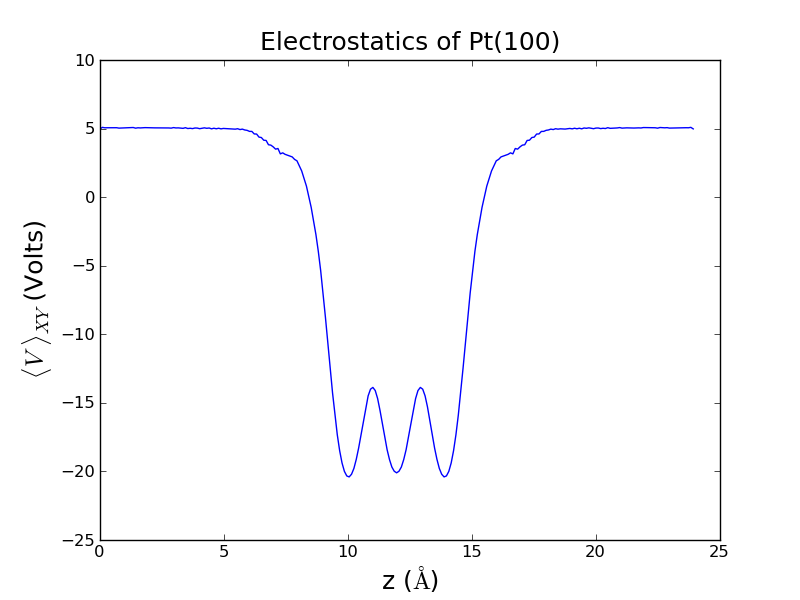
####################################################### ## Tutorial by: Andrew ## Topic: Plotting electrostatic potential data from ## ase-espresso ## ## dependencies: pickle, pylab, numpy ## ## Plots an XY-averaged electrostatic potential as ## a function of Z position through and outside ## a Pt(100) slab. ####################################################### # Import necessary packages import pickle import pylab as plt import numpy as np # Retrieves the data generated in the previous script potential_file = open('potential.pickle') potential = pickle.load(potential_file) origin=potential[0] # [X0,Y0,Z0] - The positions of the origin of the cell. Here they are [0,0,0] cell = potential[1] # [3x3 Matrix] Contains the [x,y,z] components of the 3 cell vectors cell_x = cell[0][0] # The x component of the first cell vector (Remember: This cell is rectangular) cell_y = cell[1][1] # The y component of the second cell vector (Remember: This cell is rectangular) cell_z = cell[2][2] # The z component of the third cell vector (Remember: This cell is rectangular) v = potential[2] # Contains all real-space potential field points. ####################################################### ## Understanding the architecture of the rest of the ## data can be tricky. Using the variables presented ## here, V(x,y,z)=v[x][y][z]. ## ## First we aim to extract all the information ## available to us, based on numpy's architecture. ####################################################### n_x = len(v) # Returns the number of entries in the first subset (number of X entries) n_y = len(v[0]) # Returns the number of entries in the second subset (number of Y entries - choice of '0' was arbitrary) n_z = len(v[0][0]) # Returns the number of entries in the third subset (number of Z entries - choice of '0' was arbitrary) potential = [] # Initializes a list for average potentials # Iterate over all space to average and process potential information for z in range(n_z): temp = 0 # Will serve as a partial sum for averaging purposes for x in range(n_x): for y in range(n_y): temp+=v[x][y][z] # Sums the potential at all points in an X-Y plane temp = temp / (n_x*n_y) # Divides by the total number of points potential.append( temp ) # Stores the value for average potential at this Z position # Translates the indices of points along the Z axis into real-space positions z_coordinate = np.linspace( 0 , cell_z , n_z ) # Plots the data, formats plot plt.plot(z_coordinate, potential) plt.xlabel(r'z ($\AA$)',size=18) plt.ylabel(r'$\langle V \ \rangle_{XY}$ (Volts)',size=18) plt.title('Electrostatics of Pt(100)',size=18) # Display plot plt.show() # If you'd prefer to save the plot, highlight the line above and uncomment the line below #plt.savefig('potential_analysis.png')
The end result should look something like this: