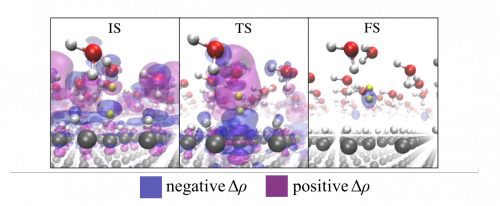
Figure: Charge density difference isosurfaces for the Heyrovsky reaction.
Electrochemical interfaces are considerably more complex than solid|gas interfaces. Solvent layers, ions, and the effect of potential are all very challenging to treat theoretically at the molecular level. In recent years, the computational hydrogen electrode model has provided an elegant way to explore thermochemical reaction energetics without explicit treatment of the electrons and ions in solution, and has provided computational screening criteria that led to the discovery of new active catalysts. However, surmountable thermochemical pathways are a necessary but not sufficient condition for activity. Proton-electron transfer barriers are required to determine kinetics and selectivity, and their determination necessitates the inclusion of the solvent and charge in the model system.
Because of the complex nature of the electrochemical interface, attempts to determine electrochemical barriers explicitly using density functional theory have emerged only in the past few years. A major challenge in the ab initio calculation of electrochemical barriers is that simulations are done at constant charge, while real electrochemical systems operate at constant potential. While it is possible to extrapolate to the constant potential limit by using very large simulation cells, it is extremely costly computationally to do so for when analyzing most electrochemical reactions. Recently, we showed that a simple electrostatic model links the energetics at constant charge to those constant potential. In this work, we show that the potential dependence of the simple proton-electron barriers is given by the shift in interfacial charge in a constant charge barrier calculation. This method allows for a tremendous reduction in the computational resources required to determine electrochemical barriers and paves the way for a rigorous DFT-based kinetic analysis of electrochemical reactions.